Introduction
When programming a game or, frankly speaking, when programming
anything, you will be confronted with intervals.
I remember reaching the point, where I began thinking about a
separate class, when I was working on the particle engine. I had about 30
values to track per particle (velocity, starting position, rotation,
acceleration...) and each one of them had an upper- and lower boundary. As I'm
not paid per line of code, I searched for a way to somehow reduce the length
and improve the readability of it (int minNumberOfParticles,
maxNumberOfParticles; float minRotation, maxRotation...).
The Interval class is a handy way to produce shorter and more
readable code while introducing a new level of consistency and, as I will
explain right now, accuracy as well.
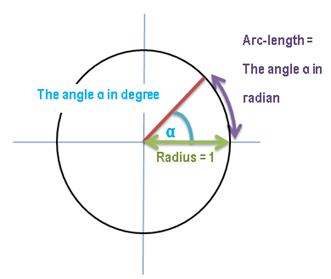
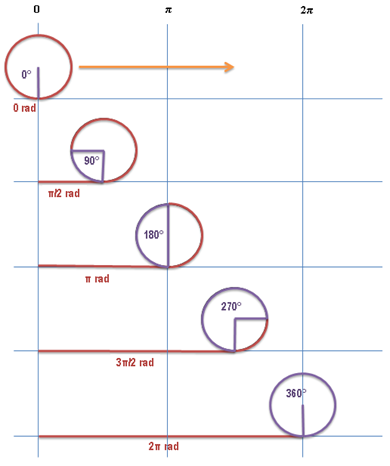
Accuracy
We don't always take care about it, but intervals don't only have
upper- and lower bounds. They also have the property to include or exclude both
bounds as well.
And when we have to take care about that, we almost certainly treat
it differently each time.
Think about it. What do you mean by: "Pick a number between 0
and 100!".
It could be one of the following:
Most
of the time we mean to include both boundaries, but we should be able to
override that behavior.
The requirements
So we want a generic class that you may instantiate using
- Only an upper and lower bound
(you would use that constructor most of the time) and it would default the
treatment of the boundaries as inclusive.
- A full constructor,
specifying the treatment of the boundaries as well
It should have convenience-methods:
- IsInBetween, that takes a
value and tells us if this given value lies within the interval
- An overload of this method,
specifying the treatment of the boundaries as well, overriding the given
treatment, but only for this single call.
- We would want it to adjust
the values in a way, that the interval doesn't become irregular
Consider you built one:
Interval<int> i = new Interval(3, 8);
And now we set the lower bound to 9. That may actually happen during
the lifetime of such an object and it may happen the other way round as well.
Our object should, without having any other useful information, do the most
sensitive thing there is to do and automatically set the upper bound to 9 as
well.
When
we think about the functionality, we should restrict the generic type-usage of
this class to the interface IComparable, which allows us to do all the proper
comparisons.
The class/struct
After writing it I saw that I used it almost everywhere and since I
was programming a game at the moment, the effort for the garbage collector was
some concern. So I found that I could change it from a class to a struct (= no
garbage collector overhead), without any side effects.
It doesn't change the way you use it at all.
The consequences
After
using it for a while now I found that the usage of this class helps making my
code a lot leaner.
For
example it reduced the LOC of my Particle class almost to half and it reduced
the number of overloads for a few different classes as well .
Think
about a randomizer-class, that gives you a random number between two given
values (which I was very lucky to have when trying to change my code to support
several multiplayer modes... Deterministic Lockstep is the keyword... But that
is another story waiting to be told).
References